SOAL Matematika Kelas 8 SMP Tentang Kerucut Lengkap Jawaban dan Pembahasan Latihan UAS/Ulangan
Makanya pastikan untuk mengikuti seluruh soal dengan seksama agar bisa lebih memahami seputar soal Matematika tentang kerucut.
TRIBUNPONTIANAK.CO.ID - Berikut pembelajaran soal latihan Matematika Kelas 8 tentang kerucut.
Terdiri dari sejumlah soal yang sudah dilengkapi dengan jawaban dan pembahasannya.
Jadi tinggal ikuti seluruh soal untuk mendapatkan pengetahuan dan wawasan.
Sehingga nantinya akan terbiasa dalam menghadapi ujian sekolah.
Soal terdiri dari soal yang membahasa tentang bangun kerucut.
Perhitungan luas serta keseluruhan dari kerucut itu sendiri.
Makanya pastikan untuk mengikuti seluruh soal dengan seksama agar bisa lebih memahami seputar soal Matematika tentang kerucut.
Baca juga: Soal dan Kunci Jawaban Matematika Kelas 5 SD Kurikulum Merdeka, STS PTS UTS Semester Genap 2024
Soal Matematika Kelas 8 Tentang Kerucut
1. Tentukan luas permukaan dan volume dari bangun kerucut berikut (lihat gambar di buku).
a. s = √(r⊃2; + t⊃2;)
s = √(4⊃2; + 12⊃2;)
s = √(16 + 144)
s = √160 = 4√10
Lp = πr(r + s)
Lp = 3,14 x 4(4 + 4√10)
Lp = 12,56(16,65)
Lp = 209,11 cm⊃2;
V = ⅓ πr⊃2;t
V = ⅓ x 3,14 x 4⊃2; x 12
V = 200,96 cm⊃3;
b. t = √(s⊃2; - r⊃2;)
t = √(10⊃2; - 6⊃2;)
t = √(100 - 36)
t = √64 = 8
Lp = πr(r + s)
Lp = 3,14 x 6(6 + 8)
Lp = 18,84(14)
Lp = 263,76 cm⊃2;
V = ⅓ πr⊃2;t
V = ⅓ x 3,14 x 6⊃2; x 8
V = 301,44 cm⊃3;
c. s = √(r⊃2; + t⊃2;)
s = √(6⊃2; + 10⊃2;)
s = √(36 + 100)
s = √136 = 2√34
Lp = πr(r + s)
Lp = 3,14 x 6(6 + 2√34)
Lp = 18,84(17,66)
Lp = 332,75 cm⊃2;
V = ⅓ πr⊃2;t
V = ⅓ x 3,14 x 6⊃2; x 10
V = 376,8 cm⊃3;
d. t = √(s⊃2; - r⊃2;)
t = √(25⊃2; - 7⊃2;)
t = √(625 - 49)
t = √576 = 24
Lp = πr(r + s)
Lp = 22/7 x 7(7 + 25)
Lp = 22(32)
Lp = 704 cm⊃2;
V = ⅓ πr⊃2;t
V = ⅓ x 22/7 x 7⊃2; x 24
V = 1232 cm⊃3;
e. r = √(s⊃2; - t⊃2;)
r = √(4⊃2; - 3⊃2;)
r = √(16 - 9)
r = √7
Lp = πr(r + s)
Lp = 3,14 x √7(√7 + 4)
Lp = 8,31(6,65)
Lp = 55,23 cm⊃2;
V = ⅓ πr⊃2;t
V = ⅓ x 22/7 x (√7)⊃2; x 3
V = 22 cm⊃3;
f. t = √(s⊃2; - r⊃2;)
t = √(13⊃2; - 5⊃2;)
t = √(169 - 25)
t = √144 = 12
Lp = πr(r + s)
Lp = 3,14 x 5(5 + 13)
Lp = 15,7(18)
Lp = 282,6 cm⊃2;
V = ⅓ πr⊃2;t
V = ⅓ x 3,14 x 5⊃2; x 12
V = 314 cm⊃3;
2. Tentukan panjang dari unsur kerucut yang ditanyakan (lihat gambar di buku).
a. V = ⅓ πr⊃2;t
t = V x 3 : (πr⊃2;)
t = 300π x 3 : (π x10⊃2;)
t = 900 : 100 = 9 m
b. V = ⅓ πr⊃2;t
r⊃2; = (V x 3) : πt
r⊃2; = (120π x 3) : π10
r⊃2; = 360π : 10π
r⊃2; = 36
r = √36 = 6 m
t = √(s⊃2; - r⊃2;)
t = √((14,5)⊃2; - 8⊃2;)
t = √(210,25 - 64)
t = √146,25
t = 12,09 cm
d. r = √(s⊃2; - t⊃2;)
r = √(15⊃2; - 12⊃2;)
r = √(225 - 144)
r = √81 = 9 dm
e. Lp = πr(r + s)
225π = πr(r + 16)
225 = r(r + 16)
225 = r⊃2; + 16r
r⊃2; + 16r - 225 = 0
(r + 25)(r - 9) = 0
r = -25 atau r = 9
maka nilai r = 9
t = √(16⊃2; - 9⊃2;)
t = √(256 - 81)
t = √175 = 5√7
f. V = ⅓ πr⊃2;t
t = V x 3 : (πr⊃2;)
t = 150π x 3 : (π(7,5)⊃2;)
t = 450π : π(56,25)
t = 450 : (56,25) = 8 cm
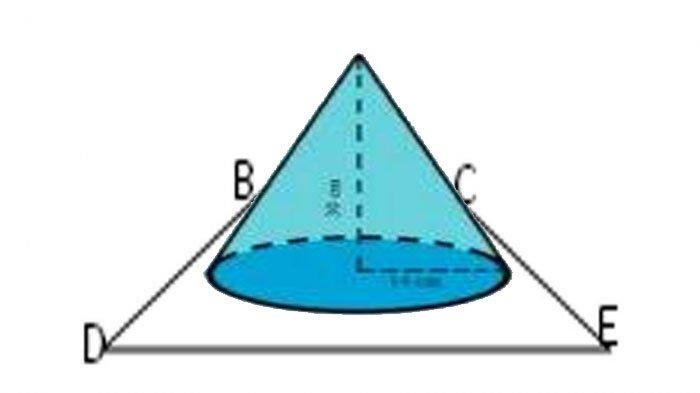
3. Tumpeng. Pada suatu hari Pak Budi melakukan syukuran rumah baru. Pak Budi memesan suatu tumpeng. Tumpeng tersebut memiliki diameter 36 cm dan tinggi 24 cm.
Namun, diawal acara Pak Budi memotong bagian atas tumpeng tersebut secara mendatar setinggi 8 cm. Berapakah luas permukaan dan volume dari tumpeng yang tersisa?
d1 = 36 cm -> r1 = 18 cm
t1 = 24 cm
t2 = 8 cm
d2 = 8/24 x 36 = 12 cm -> r2 = 6 cm
s1 = √(r1⊃2; + t1⊃2;)
s1 = √(18⊃2; + 24⊃2;)
s1 = √(324 + 576)
s1 = √900 = 30 cm
s2 = √(r2⊃2; + t2⊃2;)
S2 = √(6⊃2; + 8⊃2;)
S2 = √(36 + 64)
S2 = √100 = 10 cm
Lp = L alas tumpeng + L alas potongan + L selimut tumpeng - L selimut potongan
Lp = π.18⊃2; + π.6⊃2; + π.18.(18+30) - π.6.(6+10)
Lp = 324π + 36π + 864π - 96π
Lp = 1128π
V sisa = Vt - Vp
V sisa = ⅓ π.r1⊃2;.t1 - ⅓ π.r2⊃2;.t2
V sisa = ⅓ π.18⊃2;.24 - ⅓ π.6⊃2;.8
V sisa = 2592π - 96π = 2496π
4. Suatu kerucut memiliki jari-jari 6 cm dan tinggi t cm. Jika luas permukaan kerucut adalah A cm⊃2; dan volume kerucut adalah A cm⊃3; maka tentukan:
r = 6 cm
t = t
Lp = A cm⊃2;
V = A cm⊃3;
s = √(r⊃2; + t⊃2;) = √(6⊃2; + t⊃2;) = √(36 + t⊃2;)
a. Nilai dari t.
Lp = V
πr(r + s) = ⅓ πr⊃2;t
6(6 + s) = ⅓ 6⊃2;t
(6 + s) = ⅓ x 6 x t
6 + √(36 + t⊃2;)= 2t
√(36 + t⊃2;) = 2t - 6
36 + t⊃2; = 4t⊃2; - 24t + 36
t⊃2; = 4t⊃2; - 24t
4t⊃2; - t⊃2; - 24t = 0
3t⊃2; - 24t = 0
t⊃2; - 8t = 0
t(t - 8) = 0
t = 0 atau t = 8
b. Nilai dari A.
V = ⅓ πr⊃2;t
A = ⅓ π.6⊃2;.8
A = 96π
5. Terdapat suatu bangun ruang yang diperoleh dari dua kerucut yang sepusat. Kerucut yang lebih besar memiliki jari-jari 10 cm dan tinggi 24 cm.
Jari-jari kerucut kecil adalah ½ jari-jari kerucut besar. Tinggi kerucut kecil adalah ½ tinggi kerucut besar (lihat gambar di buku)
r1 = 10 cm
t1 = 24 cm
r2 = ½.r1 = 5 cm
t2 = ½.t1 = 12 cm
s1 = √(r⊃2; + t⊃2;) = √(10⊃2; + 24⊃2;) = √(100 + 576) = √676 = 26
s2 = √(r⊃2; + t⊃2;) = √(5⊃2; + 12⊃2;) = √(25 + 144) = √169 = 13
Tentukan:
a. luas permukaan
L = L selimut besar + L selimut kecil + L alas besar - L alas kecil
L = πrs + πrs + πr⊃2; - πr⊃2;
L = π.10.26 + π.5.13 + π.10⊃2; - π.5⊃2;
L = 260π + 65π + 100π - 25π = 400π cm⊃2;
b. volume.
V = V besar - V kecil
V = ⅓ π.10⊃2;.24 - ⅓ π.5⊃2;.12
V = 800π - 100π = 700π cm⊃3;
Dapatkan Informasi Terkini dari Tribun Pontianak via SW di sini
Cek berita dan artikel menarik lainnya melalui akses Google News
| 45 TOP Soal Latihan Ujian Sekolah PKWU Kelas 12 Kurikulum Merdeka dan Kunci Jawaban |

|
|---|
| Kunci Jawaban PAI Kelas 7 SMP Kurikulum Merdeka Halaman 4 Bab 1 Pantun Pemantik |

|
|---|
| 40 TOP Soal Ujian PJOK Kelas 3 SD, Lengkap Kunci Jawaban Baru Kurikulum Merdeka |

|
|---|
| 45 TOP Soal Ujian Bahasa Indonesia Kelas 3 SD/MI Semester 1 Lengkap dengan Kunci Jawaban |

|
|---|
| SOAL Ulangan PJOK Kelas 1 SD Semester 1 Lengkap Kunci Jawaban Persiapan Ujian & Referensi Soal Guru |

|
|---|















Isi komentar sepenuhnya adalah tanggung jawab pengguna dan diatur dalam UU ITE.